强化学习中的 TD 方法
目录
时序差分方法 (TD) 结合 Sample 和 Bootstrapping
时序差分 (Temporal-Difference, TD) 方法结合了强化学习中的两大关键思想: Sample Updates 和 Bootstrapping.它融合了蒙特卡罗方法 (MC) 的优势和动态规划 (DP) 的特点.我们分别从这两个概念出发, 详细说明 TD 方法是如何同时结合它们的.
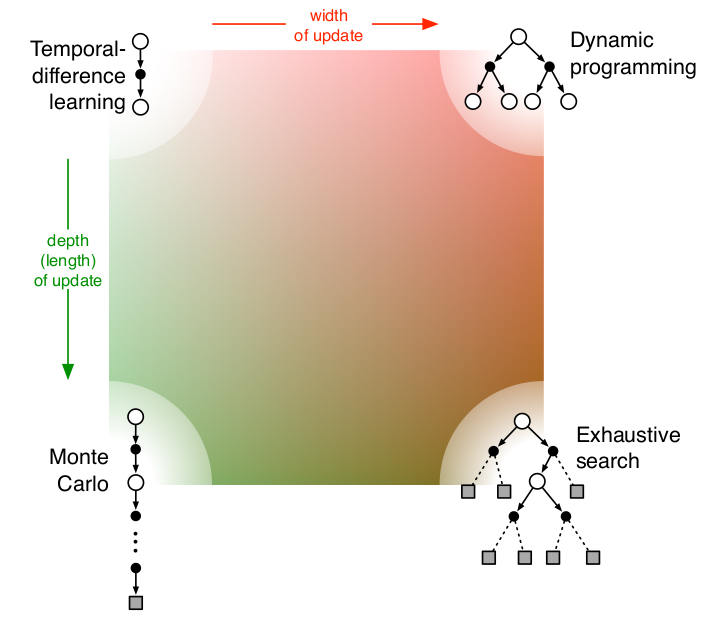
Sample Updates
样本更新指的是基于从环境中采样得到的实际数据 (真实交互样本) 来更新价值函数, 而不是计算所有可能状态或动作的期望值.
在蒙特卡罗方法中, 更新价值函数完全依赖于采样轨迹的真实回报.例如:
蒙特卡罗更新公式:
$$
V(s_t) \gets V(s_t) + \alpha \big[ G_t - V(s_t) \big]
$$
其中, $G_t$ 是从时间步 $t$ 开始的完整回报 (即所有未来奖励的累积和), $\alpha$ 是学习率.
特点: 样本更新只需要从环境中采样, 而不需要知道环境的状态转移概率 $P(s'|s,a)$ 或奖励函数 $R(s,a,s')$.
TD 方法中的样本更新
TD 方法同样基于从环境中采样得到的实际数据 (单步交互样本) : 当前状态 $s_t$、动作 $a_t$、即时奖励 $R_{t+1}$ 和下一个状态 $s_{t+1}$.这些数据来源于与环境的交互.
TD 更新公式:
$$
V(s_t) \gets V(s_t) + \alpha \big[ R_{t+1} + \gamma V(s_{t+1}) - V(s_t) \big]
$$
$R_{t+1}$ 和 $s_{t+1}$ 是从环境中交互得到的真实值, 体现了样本更新的特点.
Bootstrapping
利用当前的价值函数估计值来预测未来回报, 而不是等待真实的完整回报.例如在动态规划 (DP) 中, 价值函数的更新基于贝尔曼方程, 利用了状态转移概率和当前的价值估计.
动态规划更新公式:
$$
V(s) \gets \sum_a \pi(a|s) \sum_{s'} P(s'|s,a) \big[ R(s,a,s') + \gamma V(s') \big]
$$
这里的 $\sum_{s'} P(s'|s,a) [R(s,a,s') + \gamma V(s')]$ 是对未来回报的期望估计, 而不是实际采样轨迹.
特点: Bootstrapping依赖当前的价值函数估计值进行更新, 而不需要真实的完整回报.
TD 方法中的Bootstrapping
TD 方法利用当前价值函数估计值 $V(s_{t+1})$ 来预测未来的回报, 而不是等到任务结束后计算完整的累积回报 $G_t$.
TD 更新目标:
$$
\text{TD Target} = R_{t+1} + \gamma V(s_{t+1})
$$
这一目标结合了即时奖励 $R_{t+1}$ 和对未来奖励的估计值 $V(s_{t+1})$.
TD 方法基于此目标更新当前状态的价值函数:
$$
V(s_t) \gets V(s_t) + \alpha \big[ \underbrace{R_{t+1} + \gamma V(s_{t+1}}_{\text{TD Target}}) - V(s_t) \big]
$$
体现 Bootstrapping 的特点: $V(s_{t+1})$ 是一个估计值, 而不是完整的回报.这种依赖于当前价值函数的更新方式就是Bootstrapping.
TD 如何结合 Sample 和 Bootstrapping?
TD 方法的更新公式:
$$
V(s_t) \gets V(s_t) + \alpha \big[ R_{t+1} + \gamma V(s_{t+1}) - V(s_t) \big]
$$
从公式中可以看出, 它同时结合了 样本更新 和 Bootstrapping 的特点:
样本更新的部分
$R_{t+1}$ 和 $s_{t+1}$ 是从实际环境中采样得到的真实数据. TD 方法不需要知道状态转移概率 $P(s'|s,a)$ 或奖励函数 $R(s,a,s')$, 只依赖于单步交互的样本.
Bootstrapping的部分
$\gamma V(s_{t+1})$ 是基于当前价值函数估计的未来回报的预测值, 而不是完整的轨迹回报. TD 方法利用了当前的价值函数估计值, 体现了Bootstrapping的思想.
对比 TD、MC 和 DP
| 特性 | 动态规划 (DP) | 蒙特卡罗方法 (MC) | 时序差分方法 (TD) |
|---|---|---|---|
| 是否需要模型 | 需要完整的环境模型 | 不需要模型 | 不需要模型 |
| 更新方式 | 基于期望更新 | 基于样本更新 | 基于样本更新和Bootstrapping相结合 |
| 是否需要完整轨迹 | 不需要 | 需要完整episode | 不需要 |
| 更新时机 | 同步更新, 所有状态同时更新 | 延迟更新, 需要等待episode结束 | 即时更新, 每一步都可以更新 |
| 计算复杂度 | 高 | 中 | 低 |
| 适用任务 | 小规模问题, 需已知模型 | 有明确episode终止的任务 | 无需模型、适用于大规模问题或持续性任务 |
TD 结合 Sample 和 Bootstrapping 的优势
无需模型
- TD 方法与 MC 方法一样, 基于交互样本更新价值函数, 不需要环境的状态转移概率或奖励函数.
实时更新
- TD 方法可以在每一个时间步更新价值函数, 而不需要等待episode结束 (像 MC 那样需要完整的回报) .
低计算复杂度
- TD 方法只需要使用单步样本和当前的价值函数估计值更新价值函数, 无需像 DP 那样计算所有可能的状态转移和动作期望.
权衡偏差与方差
- 与 MC 方法相比, TD 方法通过使用价值函数的估计值 (而不是完整回报) 减少了更新的方差.
- 与 DP 方法相比, TD 方法通过样本更新引入了一定的偏差, 但避免了对环境模型的依赖.
灵活性
- TD 方法可以扩展到多步更新 (如 TD($n$) 和 TD($\lambda$)) , 进一步平衡偏差与方差.
总结
时序差分方法的核心在于结合:
- Sample Updates: 基于单步采样的真实数据进行更新.
- Bootstrapping: 利用当前价值函数估计值预测未来回报.
这种结合使得 TD 方法既适用于无模型环境, 又可以在偏差和方差之间取得良好的权衡, 是强化学习中最重要的价值函数估计方法之一. TD 方法的实时更新特性和高效性, 使其成为许多现代强化学习算法 (如 Q-learning 和 SARSA) 的基础.